Hourglass Honeycomb Chess
This variant arose from ideas of maximising the directions in which Castling and Cathedsralling was available. The arrangement of a square back rank of even side was never ideal as its effect was to put the royally-restricted piece off-centre and so ill-positioned for Cathedralling with pieces at the ends of the back-rank diagonal not going through its cell. Conversely, a square back rank of odd side would mean having the Bishops, if Bishops they were, all on the same binding.Two options that I considered for a cubic board were to have only compound pieces - Chatelaines at the corners of the middle level, Vicereines at those of the middle filestack, Primates at the top corners of the entire cube, and Moderators at the bottom ones - and only divergent pieces - Stewardesses, Waitresses, Contrastewardesses, and Valets in the same positions. In the latter case the moves for Castling and Cathdralling would be the noncapturing ones. These two options might yet see the light of day as Crowned 3d Chess and Churlish Chess.
The idea leading to this variant, however, was to use a hex-prism board, on which Bishops themselves are unbound. As the Unicorn is very severely bound on this geometry it turns out to be an especially good 3d geometry for armies of purely 2d pieces, as described in the Honeycomb Chess page. What I was however less happy with was using progressively larger ranks than the 7x7 end ranks that were the minimum requirement for Castling and Cathedralling on eight sides. However, the Hourglass Hex Chess principle of ranks progressively decreasing in size from the ends could also be applied in 3d, and that was what I decided to do to effectively give a board of two overlapping triangiular prisma, of side 7 throughout. It is the combination of the principles of the two variants that gives this variant its name.
Honeycomb Chess itself is hex-ranked and so the same pieces can and cannot move within a rank as on square-cell boards, but Hourglass Honeycomb is hex-level and so transfers this distinction to levels. To restore pieces that cannot move within a rank I chose to fill out the spaces between the symmetric pieces with their rankers - versions of them restricted to moving more ranks than files. The Mitregi-based subvariants also use forward-only pieces.
Since the introduction of an economic way to display a wider range of piece images in arrays I have been emboldened to add a subvariant featuring Crooked pieces, and upgrade the thoughts of.Mitregi-based gamse into full subvariants.
Setup
Main variant:Levels 1 and 7:
Levels 2 and 6:
Level 3:
Level 4:
Level 5:
.
Crooked-piece variant:
Levels 1 and 7:
Levels 2 and 6:
Levels 3 and 5:
Level 4:
.
Hourglass Honeycomb Mitregi
Levels 1 and 7:
Levels 2 and 6:
Level 3:
Level 4:
Level 5:
.
Hourglass Honeycomb Wildokisaki
Levels 1 and 7:
Level 2
Level 3:
Level 4:
Level 5:
Pieces
 The KING moves one step along any of the 8 orthogonals and 12 root-2 diagonals. It is unpromotable and must be kept out of Check.
The KING moves one step along any of the 8 orthogonals and 12 root-2 diagonals. It is unpromotable and must be kept out of Check.
Most straight pieces have a ranker and a forward-only form. The linepieces also have Crooked versions. Pieces in italics are not used in these variants but are included in the table for completeness' sake. All other pieces in this table are unpromotable unless otherwise specified.
| symmetric piece | ranker | forward-only piece | Crooked piece |
|---|---|---|---|
 The QUEEN moves any distance through empty intermediate cells in the same directions as the King. The QUEEN moves any distance through empty intermediate cells in the same directions as the King. |  The QUEENRANKER moves any distance through empty intermediate cells along the 4 orthogonals, and 8 root-2 diagonals, not leaving it on the same rank. The QUEENRANKER moves any distance through empty intermediate cells along the 4 orthogonals, and 8 root-2 diagonals, not leaving it on the same rank. |  The PRINCESS moves any distance through empty intermediate cells along the 2 forward orthogonals, and 4 forward root-2 diagonals. The PRINCESS moves any distance through empty intermediate cells along the 2 forward orthogonals, and 4 forward root-2 diagonals. |  The DOUBLESCOUT differs from the Queen in that it turns 90° at each intermediate cell so that odd steps of the move are in one direction and even steps in another, always both orthogonal or both diagonal. The DOUBLESCOUT differs from the Queen in that it turns 90° at each intermediate cell so that odd steps of the move are in one direction and even steps in another, always both orthogonal or both diagonal.
|
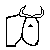 The GNU makes an unblockable leap 2 or 3 ranks and 1 level, 2 or 3 levels and 1 rank or file, or 2 or 3 files and 1 level. The GNU makes an unblockable leap 2 or 3 ranks and 1 level, 2 or 3 levels and 1 rank or file, or 2 or 3 files and 1 level. |  The GNURANKER makes an unblockable leap 2 or 3 ranks and 1 level. The GNURANKER makes an unblockable leap 2 or 3 ranks and 1 level. |  The HANDYMAN makes an unblockable leap 2 or 3 ranks forward and 1 level. The HANDYMAN makes an unblockable leap 2 or 3 ranks forward and 1 level. | |
 The ROOK moves any distance through empty intermediate cells along any of the 8 orthogonals. The ROOK moves any distance through empty intermediate cells along any of the 8 orthogonals. |  The ROOKRANKER moves any distance through empty intermediate cells along the 2 forward and 2 backward orthogonals. The ROOKRANKER moves any distance through empty intermediate cells along the 2 forward and 2 backward orthogonals. |  The WING moves any distance through empty intermediate cells along the 2 forward orthogonals. It is promotable to Goldgeneral. The WING moves any distance through empty intermediate cells along the 2 forward orthogonals. It is promotable to Goldgeneral. |  The GIRLSCOUT differs from the Rook in that it turns 90° at each intermediate cell so that odd steps of the move are in one direction and even steps in another. The GIRLSCOUT differs from the Rook in that it turns 90° at each intermediate cell so that odd steps of the move are in one direction and even steps in another. |
 The BISHOP moves any distance through empty intermediate cells along any of the 12 root-2 diagonals. The BISHOP moves any distance through empty intermediate cells along any of the 12 root-2 diagonals. |  The BISHORANKER moves any distance through empty intermediate cells along the 4 forward and 4 backward root-2 diagonals. The BISHORANKER moves any distance through empty intermediate cells along the 4 forward and 4 backward root-2 diagonals. |  The MITRE moves any distance through empty intermediate cells along the 4 forward root-2 diagonals. It is promotable to Silvergeneral. The MITRE moves any distance through empty intermediate cells along the 4 forward root-2 diagonals. It is promotable to Silvergeneral. |  The BOYSCOUT differs from the Bishop in that it turns 90° at each intermediate cell so that odd steps of the move are in one direction and even steps in another. The BOYSCOUT differs from the Bishop in that it turns 90° at each intermediate cell so that odd steps of the move are in one direction and even steps in another. |
 The KNIGHT makes an unblockable leap 2 ranks and 1 level, 2 levels and 1 rank or file, or 2 files and 1 level. The KNIGHT makes an unblockable leap 2 ranks and 1 level, 2 levels and 1 rank or file, or 2 files and 1 level. |  The NIGHTRANKER makes an unblockable leap 2 ranks and 1 level. The NIGHTRANKER makes an unblockable leap 2 ranks and 1 level. |  The HELM makes an unblockable leap 2 ranks forward and 1 level. It is promotable to Goldgeneral. The HELM makes an unblockable leap 2 ranks forward and 1 level. It is promotable to Goldgeneral. | |
 The CAMEL makes an unblockable leap 3 ranks and 1 level, 3 levels and 1 rank or file, or 3 files and 1 level. The CAMEL makes an unblockable leap 3 ranks and 1 level, 3 levels and 1 rank or file, or 3 files and 1 level. |  The CAMELRANKER makes an unblockable leap 3 ranks and 1 level. The CAMELRANKER makes an unblockable leap 3 ranks and 1 level. |  The HUMP makes an unblockable leap 3 ranks forward and 1 level. It is promotable to Silvergeneral. The HUMP makes an unblockable leap 3 ranks forward and 1 level. It is promotable to Silvergeneral. | |
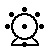 The GOLDGENERAL moves like the King but only in the 8 orthogonal, and 4 forward root-2 diagonal, directions. The GOLDGENERAL moves like the King but only in the 8 orthogonal, and 4 forward root-2 diagonal, directions. |  The COPPERGENERAL moves like the King but only in the 4 rank-changing orthogonal, and 4 forward root-2 diagonal, directions. It is promotable to Goldgeneral. The COPPERGENERAL moves like the King but only in the 4 rank-changing orthogonal, and 4 forward root-2 diagonal, directions. It is promotable to Goldgeneral. | ||
 The SILVERGENERAL moves like the King but only in the 12 root-2 diagonal, and 2 forward orthogonal, directions. The SILVERGENERAL moves like the King but only in the 12 root-2 diagonal, and 2 forward orthogonal, directions. |  The NICKELGENERAL moves like the King but only in the 8 rank-changing root-2 diagonal, and 2 forward orthogonal, directions. It is promotable to Silvergeneral. The NICKELGENERAL moves like the King but only in the 8 rank-changing root-2 diagonal, and 2 forward orthogonal, directions. It is promotable to Silvergeneral. |
 The PAWN moves one step along either forward orthogonal except when capturing, which it does one step along any of the 4 forward root-2 diagonals. It is promotable to any other capturable array piece, although promotion to anything but Queen or Gnu is an underpromotion.
The PAWN moves one step along either forward orthogonal except when capturing, which it does one step along any of the 4 forward root-2 diagonals. It is promotable to any other capturable array piece, although promotion to anything but Queen or Gnu is an underpromotion.
 The POINT moves one step along either forward orthogonal. It is promotable to Goldgeneral.
The POINT moves one step along either forward orthogonal. It is promotable to Goldgeneral.
Rules
There is no double-step initial Pawn move, and therefore no En Passant, as the Pawns are one rank less apart than in FIDE Chess.In the first two variants the King can Castle with any Rook or Cathedral with any Bishop, with both pieces moving exactly two steps. Restrictions are the standard FIDE Castling ones: both intermediate cells must be empty, they and the King cell must not be threatened by an enemy piece, and both pieces must be previously unmoved.
In the first two variants a Pawn reaching the far rank must be promoted.
In the last two variants promotable pieces may be promoted on any move entering, within,k or leaving the two ranks of the enemy camp. If a piece has no further move unpromoted, promotion is compulsory.
In the last two variants captured pieces can be reintroduced, unpromoted, in the army ofthe capturing player. Humps cannot be reintroduced on their new player's second or fifth rank, as this would make them unpromotable.
Victory is by Checkmating the enemy King.
Notes
Wildokisaki is an idea that I recently had for a 2d variant adding a Gnu and Camels as well as a Queen and Knights to Shogi. This is my provisional array:but this is contingent on suspecting that this is the array for the original Okisaki:
If anyone can confirm either way, and present the correct array if I am wrong, I will both be grateful and review my Wildokisaki array.
 This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By Charles Gilman.
Last revised by Fergus Duniho.
Web page created: 2015-08-23. Web page last updated: 2021-06-11
 The
The