Comments/Ratings for a Single Item

In 3d geometry one distinguishes body-diagonals and face diagonals.

Where is this terminology from? I am not familiar with it and have not found it anywhere I looked.

BTW, isn't it possible to cut through a cubic lattice so that you get hexagons (in a plane perpendicular to a body diagonal)?

I do not understand your terminology well enough to understand your question.

BTW, isn't it possible to cut through a cubic lattice so that you get hexagons (in a plane perpendicular to a body diagonal)?

Yep:

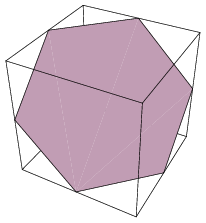
The relationship between hexagonal and cubic grids runs deeper, and in that sense hex bishops do correspond to unicorns. See e.g. https://www.redblobgames.com/grids/hexagons/#coordinates-cube

The relationship between hexagonal and cubic grids runs deeper, and in that sense hex bishops do correspond to unicorns. See e.g. https://www.redblobgames.com/grids/hexagons/#coordinates-cube

The article you linked to describes how hexes on a hexagonal grid could be described with three coordinates, because the six sides of a hexagon give it three axes. It's because of this that there is a choice when it comes to which two axes will be used to represent spaces for a particular hexagonal game, and different games have represented coordinates differently. Anyway, this article tries to make a correspondence between hexagonal grids and 3D grids, because each can be described with three coordinates. That's interesting as far as it goes, but the question remains whether there will be any correspondence between how pieces move on a 3D board and how they move on a hexagonal board. Since the article is simply about geometry and not about Chess variants, it does not cover that.

On a 3D cubic board, a Unicorn should move an equal distance in all three dimensions. So, if it starts out at (0,0,0), it could move to spaces with coordinates like (1,1,1), (2,2,2), (-1,1,-1), and so on. Looking at the diagram for axial coordinates on a hexagonal grid, the spaces that a Bishop could move to from (0,0,0) are all at a distance of 1 in two dimensions and a distance of 2 in the other dimension. These distances do not match how a Unicorn moves on a 3D board, and in fact, the grid does not contain a single hex with coordinates matching any space a Unicorn could move to from (0,0,0) on a 3D board.

I will also note that the spaces a hexagonal Bishop could reach from (0,0,0) do not match those that a 3D Bishop could reach. A 3D Bishop would be able to move to a space that is the same distance away in two dimensions but a distance of zero in the other dimension. Looking at the Axial diagram, these are on the orthogonal rows passing through (0,0,0). In other words, the way a Rook moves on a hexagonal board corresponds with the way a Bishop moves on a 3D board, at least in terms of how the coordinates change.

On a 3D board, a Knight move should adjust one coordinate by 1, one by 2, and leave the third the same. Looking at the coordinates on the Axial grid, there are no coordinates in that relation to (0,0,0). Every coordinate with no change in one coordinate has the other two at equal distances from (0,0,0). These all match the spaces a hexagonal Rook could move to.

So, in terms of Chess piece movements, I do not see much correspondence between hexagonal boards and 3D cubic boards. The changes in coordinates that Chess pieces are capable of will not be the same on each board. And even with three coordinates, the hexagonal board is missing many spaces from a 3D board and does not seem to support the sorts of coordinate changes that Rooks, Knights, and Unicorns are capable of in 3D Chess. While it supports the sort of coordinate changes Bishops are capable of, these belong to the hexagonal Rook, which can reach every space on the board.

Given all this, I do not see any way to support the idea that hexagonal Bishops correspond to 3D Unicorns. My takeaway from this is that piece movement should be defined in terms of geometric relations and not in terms of numeric coordinate changes. By defining it in terms of geometric relations, I can use the same definitions for Chess pieces on square, cubic, and hexagonal boards, and the pieces will move appropriately on each board. But if I try to define them in terms of coordinate changes, six-sided polygons (hexes) and six-sided polyhedrons (cubes) will not work the same way.

Apologies for the confusion; I had misremembered what I worked out years ago, and didn't spend much time checking how my thoughts aligned with the Red Blob site I linked.

When I've done this before, I project down along one triagonal, and the result is a hexagonal grid, but not with the "cubic coordinates" of the Red Blob site. Instead, you get coordinates whose sum is 0, 1, or 2 (any other sum in the cube coordinates get projected down to one of these, depending on its remainder mod 3), and those correspond to the 3-coloring of the hex grid. Under this projection, if my doodling just now is correct, cubic rooks are hex rooks; cubic bishops are hex rook+bishop; cubic unicorns are hex dabbabah+null-move.

That aside, I would still argue that Gilman isn't wrong in anything, but takes different definitions and reaches different conclusions. We've had games here on non-regular tesselations, and differences of opinions arise when trying to think more-topologically or more-geometrically.

The connection between the 2d and 3d moves is a projection, right? You make a 2d slice through the 3d lattice, and then projet teh trajectory of the 3d piece on it. If you take the slice parallel to the cubic lattice coordinate planes, you get a normal chess board, and 3d bishops project to normal Bishops on it. As do Unicorns. The interesting quastion is what would happen if you do that with the haxagonal slice. Neither Bishops nor Unicorns move in the slice.

If you take the slice parallel to the cubic lattice coordinate planes, you get a normal chess board, and 3d bishops project to normal Bishops on it. As do Unicorns.

The way I'm thinking about it, when you project along one of the 3d orthogonal directions, you do get a normal chess board, but 3d bishops become 2d queens, and unicorns become 2d bishops. E.g., projecting along the z direction, a 3d bishop sliding along (+1,0,+1) projects to a rook movement (+1,0).

OK, I see. And projecting a 3d Rook would give a null-move-capable 2d Rook.

But the diagonal slice through the cubic lattice does not produce a board of hexagons. If you extend the plane outside the cube you showed in the drawing, you get triangles bordering the hexagons.

The correspondence between 3D and Hex in the link is indeed not with the Cubic lattice, but with the Rhombic‐Dodecahedral one — what Gilman terms ‘Xyrixa’ (after an obscure variant of the same name) — equivalent to considering a single bishop binding of a cubic lattice in the same way that a single B binding on squares gives another square board. Thus Cubic B moves correspond to Hex/Xyrixa R moves, Cubic (2,1,1) leaps (‘Sexton’ leaps, per Punning by Numbers) to the other Hex radial, and Dabbaba leaps to Xyrixa B moves (which move off the Hex plane).

Additionally, a Sexton leap can be achieved by two Unicorn steps at right angles, as can a B step by two R steps, and the Cubic unicorn step is reachable by one R step and a perpendicular B step, as is the Hex ‘unicorn’ step on a Xyrixa board (≡ a Sexton leap by B step and perpendicular D leap). Hence an argument for unifying the two.

Of course, there is one major difference: the Hex move is arguably distinct in being not a Step, like the three Cubic radials, but a Leap like the cubic Sexton (in the sense that the cells such a move connects are not geometrically adjacent).

H.G.:

the diagonal slice through the cubic lattice does not produce a board of hexagons

Unless you do this :‌)

Not, I imagine, the worst possible board for a CV: the R moves are zigzaggy but equivalent to cubic ones, and the (proper) bishop takes (standard) diagonals — but only half of them.

I would still argue that Gilman isn't wrong in anything, but takes different definitions and reaches different conclusions.

So far, I have not addressed his math, which I will now check here:

Here is what he wrote on the page:

Standard diagonal (SD) directions, the diagonal of the standard square-cell geometry formed by simultaneously moving equal numbers of orthogonal steps at right angles have steps of length root-2. Nonstandard diagonal (ND) directions include the diagonals outside a 2d plane in the cubic geometry, colloquially called triagonal, and the diagonals of the 2d hex board. I use the same term for both as both have steps of length root-3

I now understand that by root-2 and root-3 he means the square roots of 2 and 3. For square and cubic boards, these values check out. The diagonal distance between the midpoints of two diagonally adjacent squares is the same length as the diagonal of the square itself. This is the hypotenuse of a right triangle with two of the sides. Taking each side to have a length of 1, the Pythagorean theorem gives it a length equal to the square root of 2. Likewise, the distance between the midpoint of two cubes sharing a single corner is the same as the distance between the two opposite corners of a cube. When I looked this up, I learned that it is equal to the square root of 3 times the length of one side. Giving the side a length of 1, this diagonal has a length of root-3.

Let's now consider the hexagon. When the side is equal to 1, the distance between two opposite corners will be 2, as a hexagon can be divided into six equilateral triangles sharing a common point. See How many equilateral triangles are there in a regular hexagon?. However, since there is a gap between two diagonally adjacent hexagons, this has to be added in. With a side length of 1, this gap is 1, making the total distance a Bishop travels between two diagonally adjacent hexagons as 3. Well, 3 is not its square root. So this doesn't give us the same value.

But when we start with a side length of 1, the distance a Rook moves between two adjacent squares is not 1, which is already a problem. To calculate this distance, I will refer to this Regular Hexagon Cheatsheet:

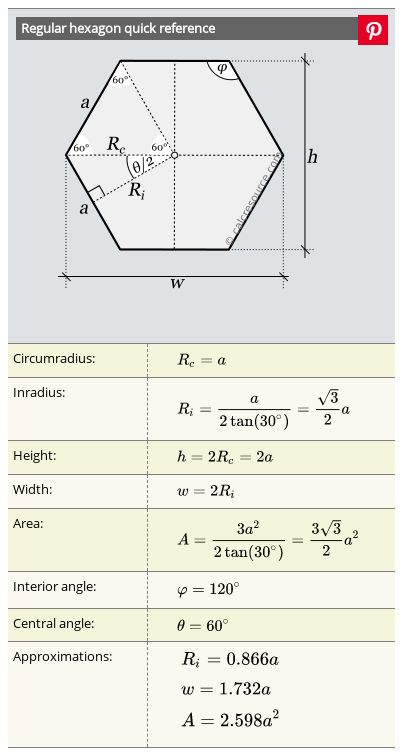
The first thing I'll do is calculate the distance between two opposite sides when a side has a length of 1. For this, we want to look at the Inradius formula for R_i. With a side length of 1, a is 1, and R_i is half the square root of 3. Since R_i is half the length we're looking for, the distance between two opposite sides is root-3, which is 1.732050807568877. So, with a side length of 1, a Rook in hexagonal Chess travels the same distance as a Unicorn in 3D Chess.

To better harmonize the distances that pieces travel on hexagonal and 3D boards, I figured it would be best to give the Rook a distance of 1 on a hexagonal board. This allows Rooks to start out traveling the same distance on each board. Since the distance between two opposite corners is twice the length of one side, I need to figure out the length of one side when the distance between opposite sides is 1. I can do this with a ratio, since I already know three of the values and can solve for the fourth. So, x is to a length of 1 as 1 is to the square root of 3. As an equation, it looks like this:

x/1 = 1/root-3

So, x = 1/root-3

Since we want three times that, we get 3 divided by its square root, which is its square root. So the math checks out.

While the math does check out, I consider this a reductio ad absurdum against his idea of defining piece movement in terms of distance. A piece that moves in all three dimensions, as a Unicorn does, cannot have any legal moves on a 2D board. Although the hexagonal Bishop moves the same distance as a 3D Unicorn, the distance a piece moves is not the same as the manner in which it moves. I conceive of the Bishop as going through 2D diagonals of polygons and of the Unicorn as going through the 3D diagonals of polyhedrons. If you change the shapes of the spaces, you are going to get different measurements, but the idea behind 2D diagonal movement and 3D diagonal movement will remain the same. In circular or spherical Chess, the measurements will even vary between different spaces on the same board, but the idea of 2D diagonal movement will still make sense when it is understood as going through the corners of spaces.

The correspondence between 3D and Hex in the link is indeed not with the Cubic lattice, but with the Rhombic‐Dodecahedral one — what Gilman terms ‘Xyrixa’

Can you expand on this? Xyrixa is a 3d geometry featuring slices that are rectangular and others that are hexagonal. Maybe the issue is that slice of the tessellation don't necessarily correspond nicely with the adjacency relation of the cells' centers?

The issue is that the ‘orthogonal’ step in the Hex lattice (between two hexes sharing a side) is identified with a Bishop step (between cubes sharing an edge but no face) on the cubic one (which I suppose is what you mean by “the adjaceny relation”?). And since all spaces on a Hex board can be reached by orthogonal steps, it follows that the 3D extrapolation is also the set of cubes reachable by such steps: a single Bishop binding (only half the cubes).

The observation that a single cubic Bishop binding corresponds to the Xyrixa board is made by Gilman a few times, f.ex. in Oddly Oblique (¶5 of the main text, following the Senhelm diagrams) and in the introduction (¶2) to OctHex 146; probably also in comments and such over the years.

Hence also the fact that a cubic Unicorn step (which is colourswitching) doesn't resolve to a Hex move with this identification (any more than a Rook step does).

huh the theme I learned two months ago)